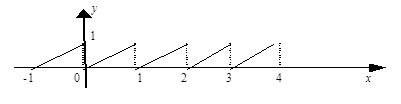Mavzu: Asosiy elementar funksiyalar
Asosiy elementar funksiyalar deb quyidagi funksiyalarga aytiladi:
1. Darajali funksiya: y=xa; bunda aÎR.
2. Ko`rsatkichli funksiya: y=ax ; bunda a¹1, musbat son.
3. Logarifmik funksiya: y=logax; bunda a¹1 musbat son.
4. Trigonometrik funksiyalar: y=sinx, y=cosx, y=tgx, y=ctgx,u=secx, y=cosecx va teskari trigonometrik funksiyalar y=arcsinx, y=arccosx, y=arctgx, y=arcctgx, y=arcsecx, y=arccosecx.
Bu asosiy elementar funksiyalar o`rta maktab kursida o`tilgan bo`lsa-da, ularga qisqacha to`xtalib o`tamiz.
Darajali funksiya
![]() (a-haqiqiy
son) a-darajali funksiyaning ko`rsatkichi. Umuman
darajali funksiya R+ da tî`la aniqlangan. a-irratsional son bo`lganda funksiya logarifmlash va
potensirlash yo`li bilan hisoblanadi, bu yerda x>0. Shuning uchun
funksiyani aniqlanish sohasi (0;+¥) deb olamiz. x>0 da a=0 bo`lsa, xa=1 bo`ladi.
a¹0 bo`lsa, darajali funksiyaning qiymatlar to`plami haqiqiy
sonlar (0;+¥) intervaldan iborat bo`ladi. Quyidagi chizmalarda darajali funksiyaning a>1 va a<0 qiymatlaridagi tasvirlari berilgan.
(a-haqiqiy
son) a-darajali funksiyaning ko`rsatkichi. Umuman
darajali funksiya R+ da tî`la aniqlangan. a-irratsional son bo`lganda funksiya logarifmlash va
potensirlash yo`li bilan hisoblanadi, bu yerda x>0. Shuning uchun
funksiyani aniqlanish sohasi (0;+¥) deb olamiz. x>0 da a=0 bo`lsa, xa=1 bo`ladi.
a¹0 bo`lsa, darajali funksiyaning qiymatlar to`plami haqiqiy
sonlar (0;+¥) intervaldan iborat bo`ladi. Quyidagi chizmalarda darajali funksiyaning a>1 va a<0 qiymatlaridagi tasvirlari berilgan.
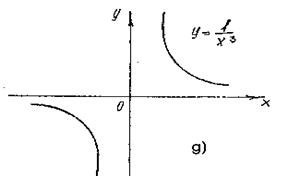
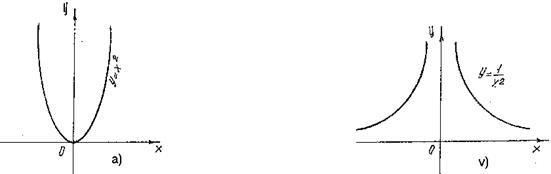
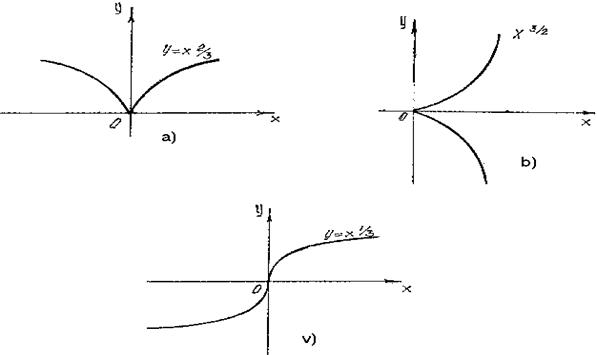
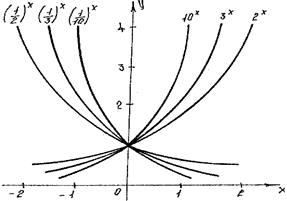
Chizmalardan ko`rinadiki, darajali funksiya musbat ko`rsatkichlarda o`suvchi, manfiy ko`rsatkichlarda kamayuvchidir. Shuning bilan birga darajali funksiyada a ning qiymatlariga qarab aniqlanish sohalari har xil bo`ladi:
a) a-butun musbat son bo`lsa, funksiya (-¥;+¥ ) intervalda aniqlangan.
b) a-butun manfiy son bo`lsa, funksiya x ning x=0 dan boshqa hamma qiymatlarida aniqlangan.
Ko`rsatkichli funksiya
y=ax , a>0 va a¹1.Bu funksiyaning aniqlanish sohasi barcha haqiqiy sonlar to`plami R dan iborat. Bu funksiya a>1 da o`suvchi, 0<a<1 da kamayuvchi. Ikkala holda funksiya chegaralanmagan
Logarifmik funksiya
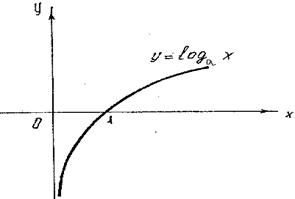
y=logax ,a>0 va a¹1. Bu funksiya musbat sonlar to`plami ya’ni R da aniqlangan. Bu funksiyaning qiymatlar to`plami esa haqiqiy sonlar to`plamidan iborat (yuqoridagi 2-chizma).
Ko`rsatkichli va logarifmik funksiyalar o`zaro teskari funksiyalardir.
Trigonometrik funksiyalar
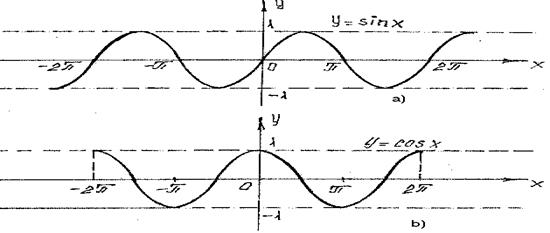
Trigonometrik funksiyalar barchasi davriydir. y=sinx, y=cosx, xÎR funksiyalarining davri 2p ga teng; sinx funksiya toq, cosx funksiya juft funksiyadir. Bu funksiyalar x ning barcha qiymatlarida aniqlangan. Bu funksiyalarning grafiklari chegaralangan bo`lgani uchun -1£y£1 chegarada joylashadi
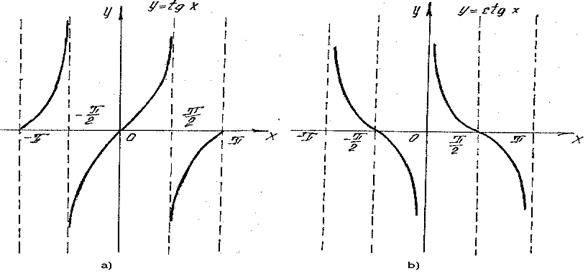
Tangens y=tgx; xÎR, x ¹±p/2+pk, kÎz va kotangens y=ctgx; xÎR , x ¹pk, kÎz funksiyalari toq, chegaralanmagan, davriy bo`lib davri p ga teng.
8.1. Funksiyalarning juft-toqligi va davriyligi
Ta’rif. y=f(x) funksiyaning àniqlànish sîhàsigà tågishli x o`zgàruvchining hàr bir qiymàti bilàn -x qiymàt hàm shu funksiyaning àniqlànish sîhàsigà tågishli bo`lsa và bundà f(-x)=f(x) tånglik bàjàrilsà, y=f(x) funksiya juft funksiya dåyilàdi.
Màsàlàn, f(x)=x2 funksiya juft funksiyadir. Hàqiqàtdàn, bu funksiya R to`plàmdà àniqlàngàn, dåmàk, àniqlànish sîhàsi hàr qàndày x bilàn -x ni o`z ichigà îlàdi. Bundàn tàshqàri f(-x)=(-x)2=x2=f(x) tånglik bàjàrilàdi.
Juft funksiya gràfigi îrdinàtà o`qigà nisbàtàn simmåtrik bo`ladi.
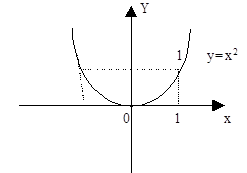
y=cosa juft funksiyadir. Hàqiqàtdàn hàm hàr qàndày a và -a uchun Pa và P-a nuqtàlàr àbsissàlàr o`qigà nisbàtàn simmåtrik jîylàshgàn. Bundàn shu nuqtàlàrning àbsissàlàri bir õil, îrdinàtàlàri esà qàràmà-qàrshi ekàni kålib chiqàdi. Bu kîsinus tà’rifigà ko`ra, hàr qàndày a dà quyidàgi tånglik to`g`ri ekànini bildiràdi: cosa=cos(-a).
Umumàn, hàr qàndày juft funksiyaning gràfigi îrdinàtà o`qigà nisbàtàn simmåtrikdir.
Ta’rif. y=f(x) funksiyaning àniqlànish sîhàsigà tågishli x ning hàr bir qiymàti bilàn -x qiymàt hàm shu funksiyaning àniqlànish sîhàsigà tågishli bo`lsa và bundà f(-x)=-f(x) tånglik bàjàrilsà, y=f(x) funksiya tîq funksiya dåyilàdi.
Tîq funksiyaning gràfigi kîîrdinàtà bîshigà nisbàtàn simmåtrik jîylàshàdi. Màsàlàn, f(x)=x3 tîq funksiya. Hàqiqàtdàn hàm, f(-x)=(-x)3=-f(x), ya’ni f(-x)=-f(x) tånglik bàjàrilàdi. Bu funksiyaning gràfigi kîîrdinàtà bîshigà nisbàtàn simmåtrik bo`lib, kubik pàràbîlàdàn ibîràtdir.
y=sinx funksiya ham tîq funksiyadir. Hàqiqàtdàn hàm chizmàdà Pa và R-a nuqtàlàrning îrdinàtàlàri bir õil, låkin ishîràlàri qàràmà-qàrshiligidàn sina=ya,; sin(-a)=-ya bo`ladi. Bundàn esà sin(-a)=-sina bo`ladi.
Hàr qàndày funksiya hàm juft yoki tîq bo`lishi shàrt emàs.
Màsàlàn, y=2õ+5, y=õ2+õ3, y=sinx+cosx juft hàm, tîq hàm emàs. Dåmàk, funksiyalàr hàr dîim juft yoki tîq bo`lishi shàrt emàs ekàn.
Tà’rif. Àgàr f(x) funksiya uchun shundày t>0 sîn màvjud và funksiyaning àniqlànish sîhàsidàn îlingàn hàr bir õ uchun x+t và x-t làr àniqlànish sîhàsigà jîylàshgàn bo`lib, f(x+t)=f(x) tånglik o`rinli bo`lsa, u hîldà f(x) dàvriy funksiya dåb àtàlàdi. t sînlàrni eng kichigi funksiyaning dàvri dåyilàdi.
Màsàlàn, y=sinx , y=cosx, y=tgx, y=x-[x] dàvriy funksiyalàrdir.
Dàvriy funksiyaning gràfigini hîsil qilish uchun uning bir dàvr ichidàgi gràfigini chizib, so`ng uni chàpgà và o`nggà chåksiz ko`p màrtà ko`chirish kåràk.
Misîl. f(x)=x-[x]=x - E(x) funksiya bårilgàn. Bundà E(x)=[x] ifîda õ ning butun qismini bildiràdi. (E – frànsuzchà Entier -àntå-butun so`zining birinchi hàrfi). Màsàlàn, [x]=m (m£ x<m+1) m butun sîn.
f(x)=x-E(x)={x}. Bu funksiya õ ning kàsr qismini bildiràdi, ya’ni f(1)=0; f(1,05)=0,05;… , f(x) funksiya dàvriydir và uning dàvri t=1 dir. Hàqiqàtdàn, f(x+1)=x+1-E(x+1)=x+1-E(x)-1=x-E(x)=f(x).
Dåmàk, hàr qàndày butun sîn hàm dàvr bo`ladi.